Visualizing marginal effects in sdmTMB models with ggeffects

If the code in this vignette has not been evaluated, a rendered version is available on the documentation site under ‘Articles’.

The package ggeffects can be used to plot marginal effects of given predictor variables in sdmTMB models.

A advantage to this approach over visreg, is that ggeffects calculates marginal effects with the effects package using the parameter covariance matrix. This is nearly instant compared to visreg, which has to calculate conditional effects by calculating predictions with TMB.

A disadvantage to using ggeffects is that it will only work for regular linear effects in the main model formula. I.e., it will not work with smoothers (internally these are random effects) or breakpoint (breakpt()) effects.

Another important distinction is that ggeffects::ggeffect() is plotting marginal effects. This means the effects are “marginalized” or “averaged” over the other fixed effects. visreg::visreg() is plotting conditional effects. This means they are conditional on the other predictors being set to certain values. ggeffects::ggpredict() also does conditional effects, but this has not yet been set up in sdmTMB using the CRAN version of ggeffects.

library(sdmTMB)
library(ggeffects)

Example with Pacific cod presence

To start, we will use the Pacific cod example data. We will fit a model of fish presence/absence with covariates of depth and a fixed effect of year using a Tweedie distribution.

pcod$fyear <- as.factor(pcod$year)
mesh <- make_mesh(pcod, c("X", "Y"), cutoff = 20)
fit <- sdmTMB(present ~ poly(depth, 2) + fyear,
  data = pcod,
  mesh = mesh,
  spatial = "on",
  family = binomial()
)

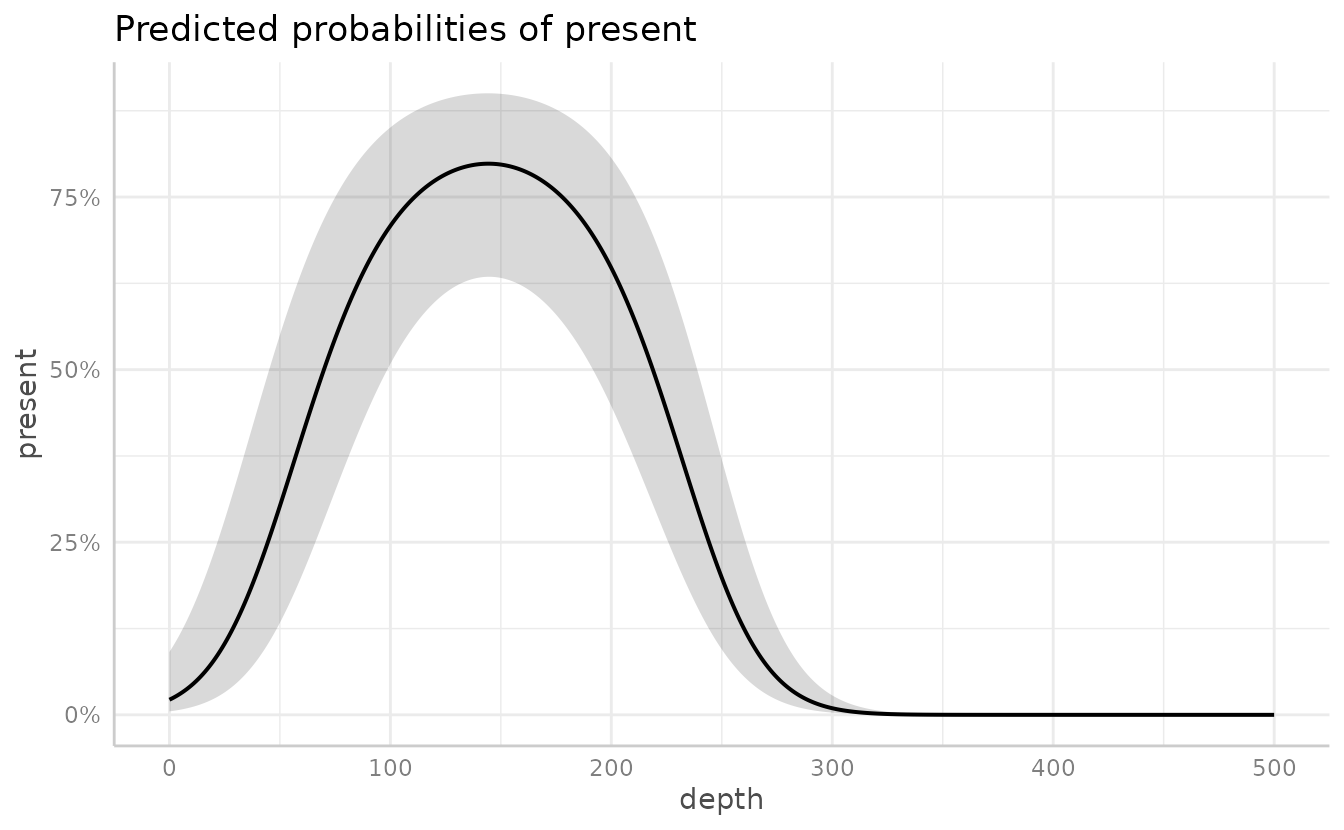
We can then use ggeffects::ggeffect() to see the effect of depth on the probability of Pacific cod being present. We can control what range and interval of depths are predicted within the function (e.g. [0:500 by=1]).

g <- ggeffect(fit, "depth [0:500 by=1]")
plot(g)

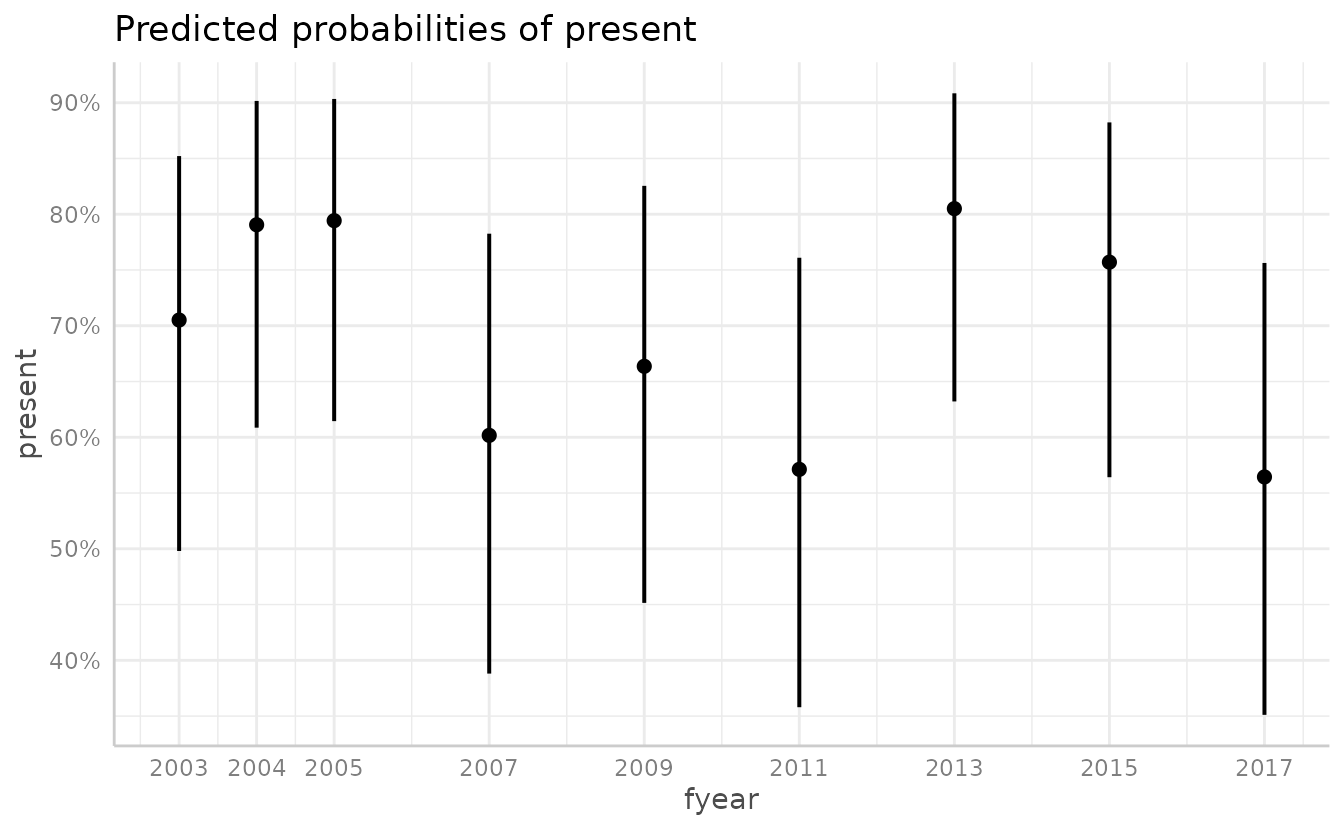
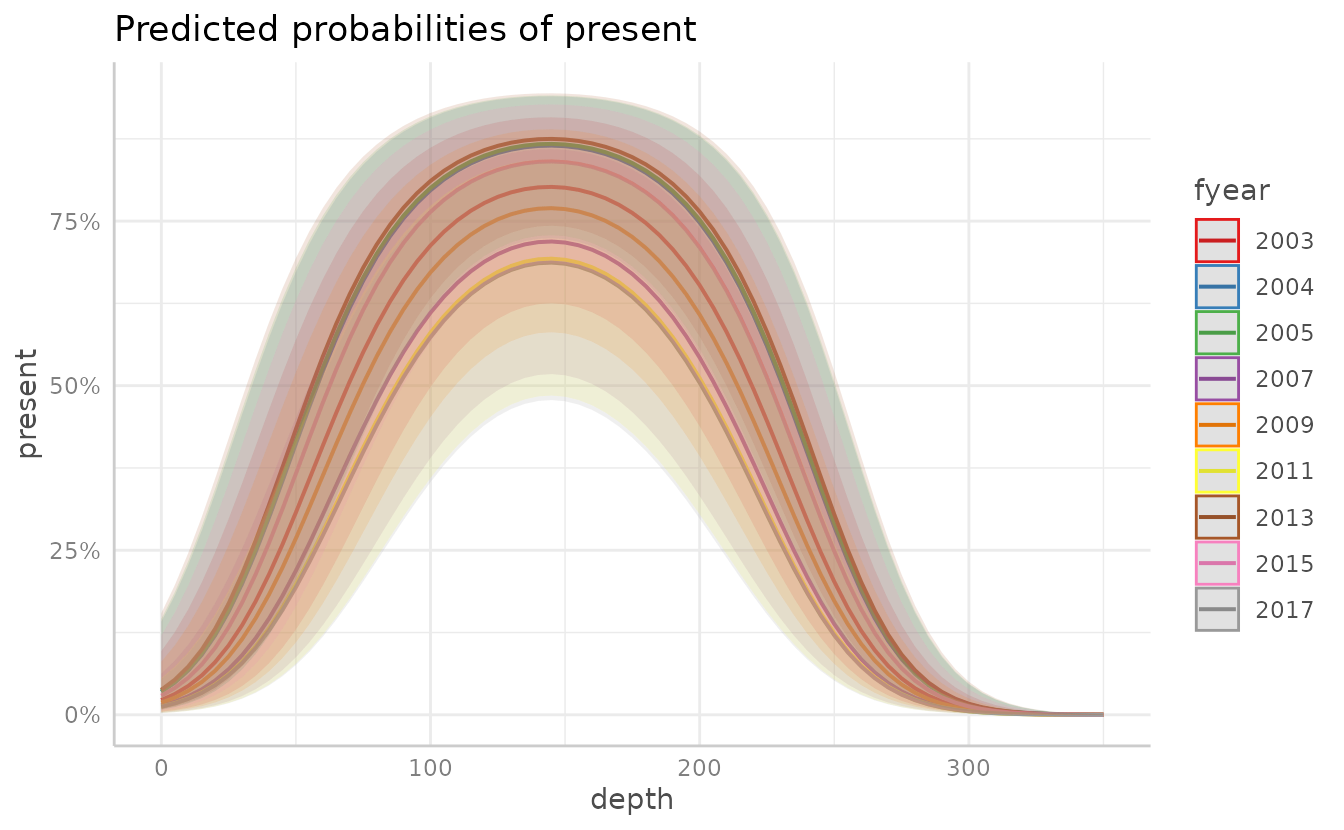
We can also plot the effects of each year.

g2 <- ggeffect(fit, "fyear")
plot(g2)

We can add in data points

plot(g, add.data = TRUE)
#> Warning: Argument `add.data` is deprecated and will be removed in the future.
#>   Please use `show_data` instead.
#> Data points may overlap. Use the `jitter` argument to add some amount of
#>   random variation to the location of data points and avoid overplotting.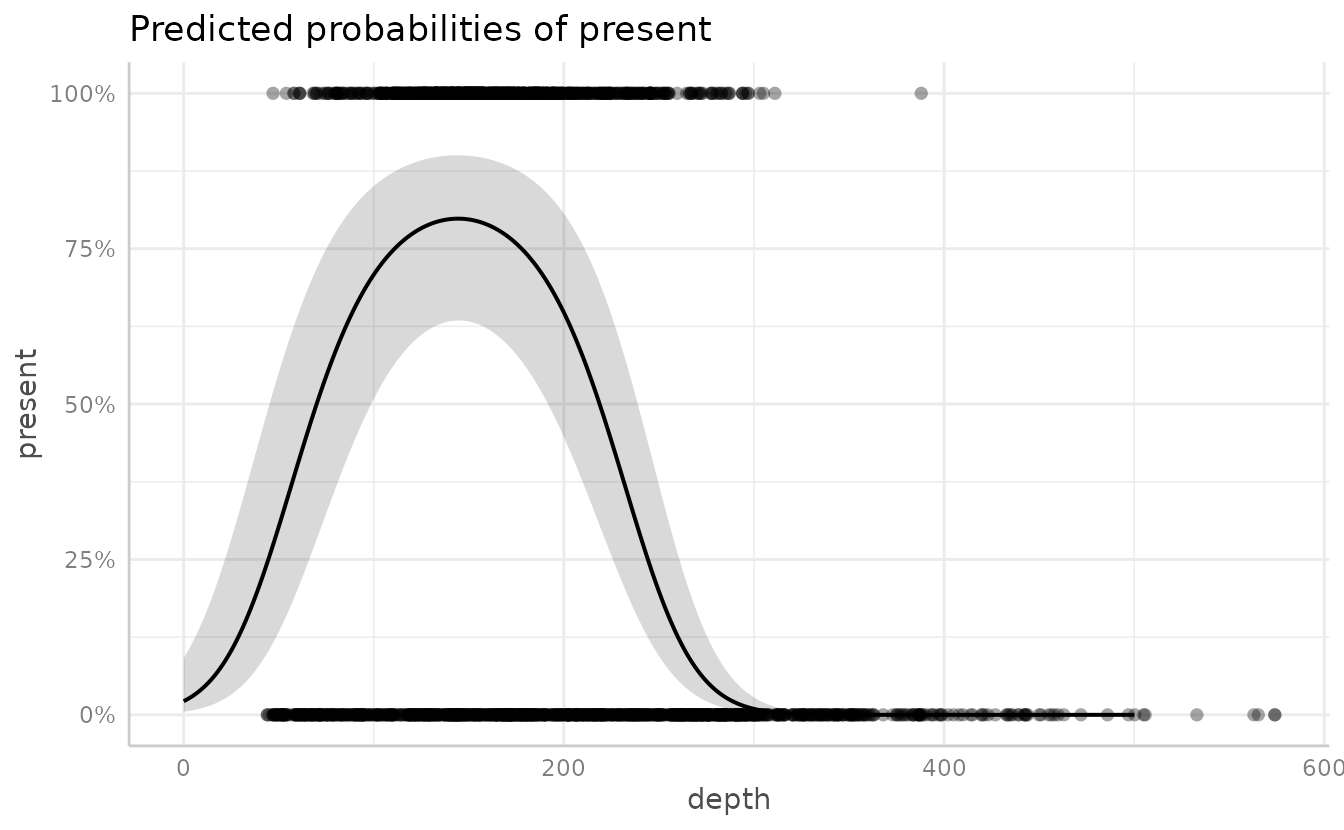

We can also use ggeffect to plot multiple variables by listing them in terms = c(), with the first term listed indicating the variable to be plotted on the x-axis, and the remaining listed terms (up to four total) indicating the groups. Adding facet = TRUE will show each year as a separate plot, instead of overlain on one plot.

dat <- ggeffect(fit, terms = c("depth [0:350 by=5]", "fyear"))
plot(dat)

Adding facet = TRUE will show each year as a separate plot, instead of overlain on one plot.

plot(dat, facet = TRUE)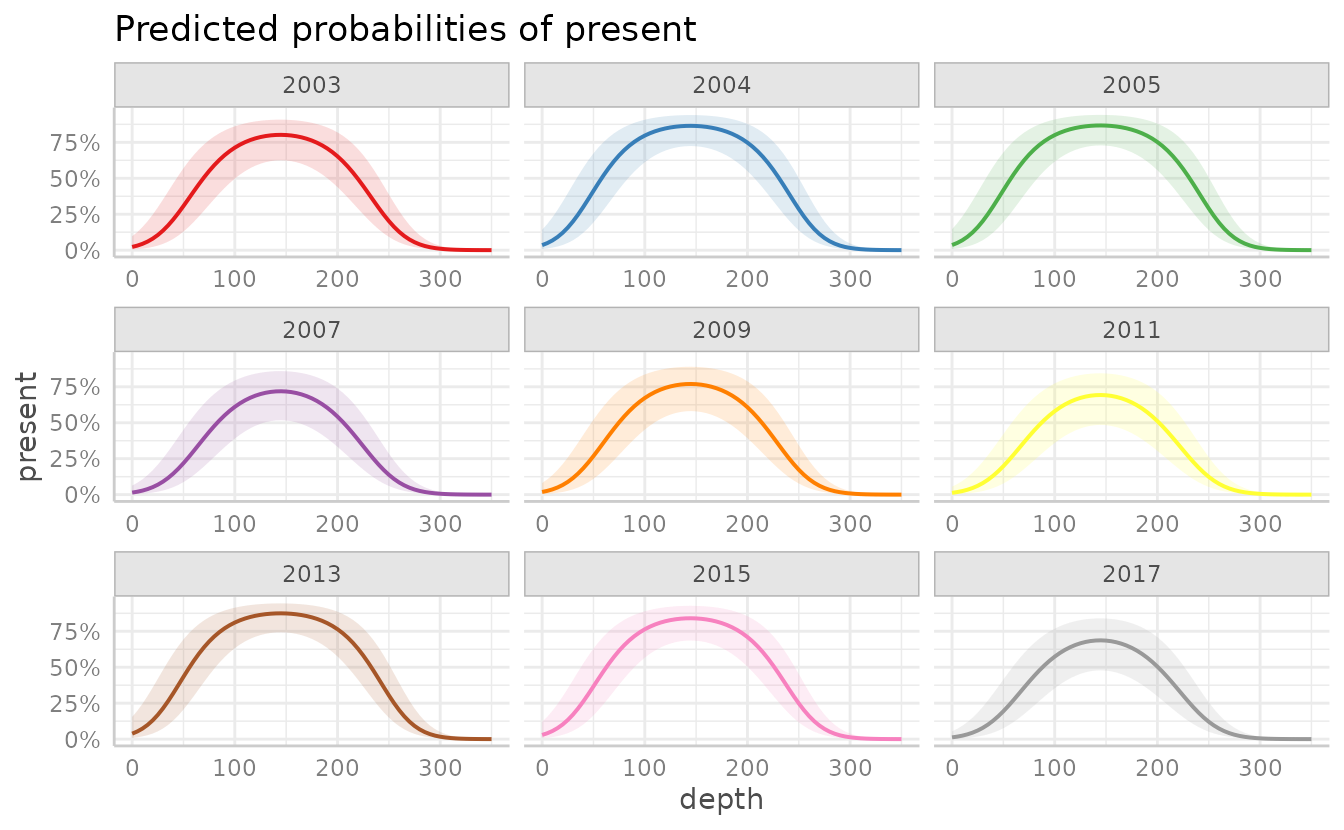

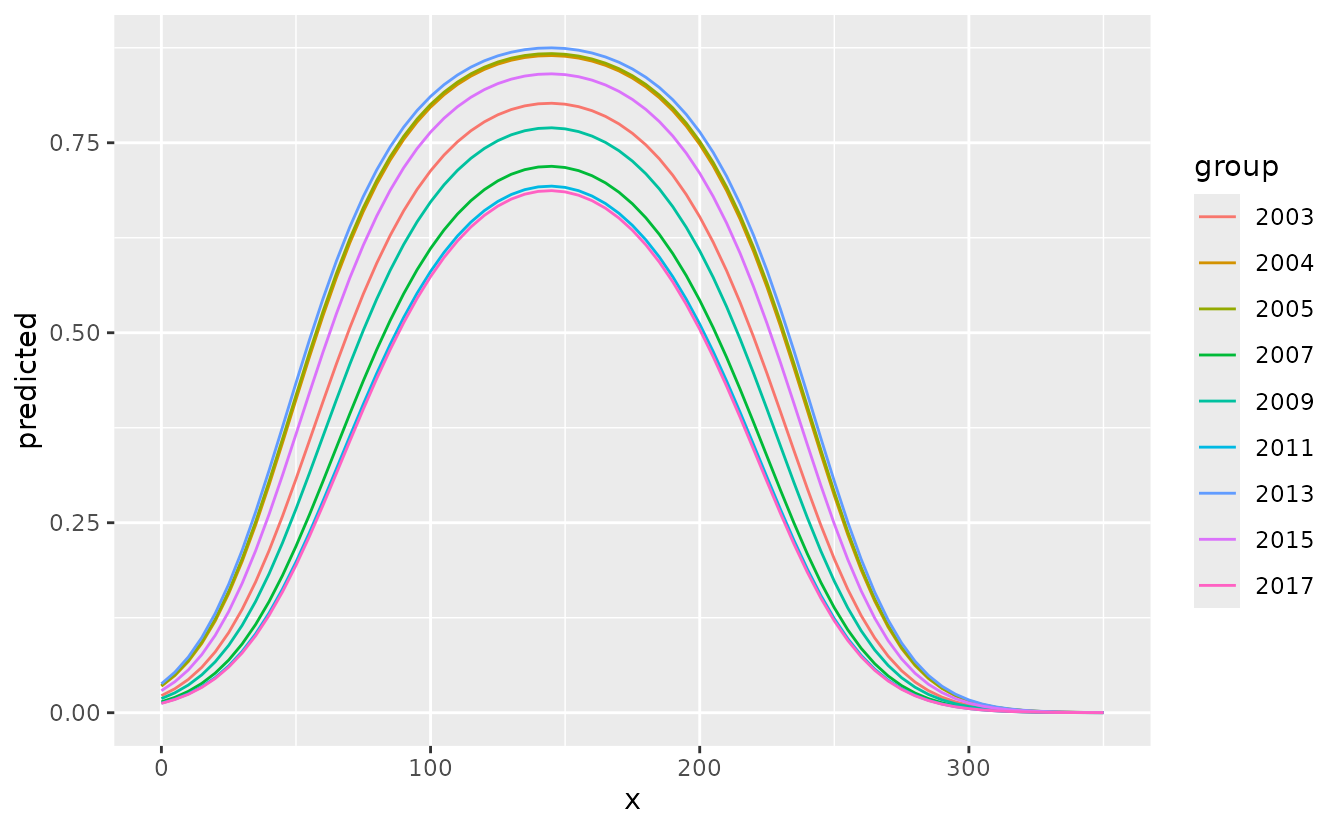
We can also use make our own ggplot plot by calling the ggeffects object dat as the data frame.

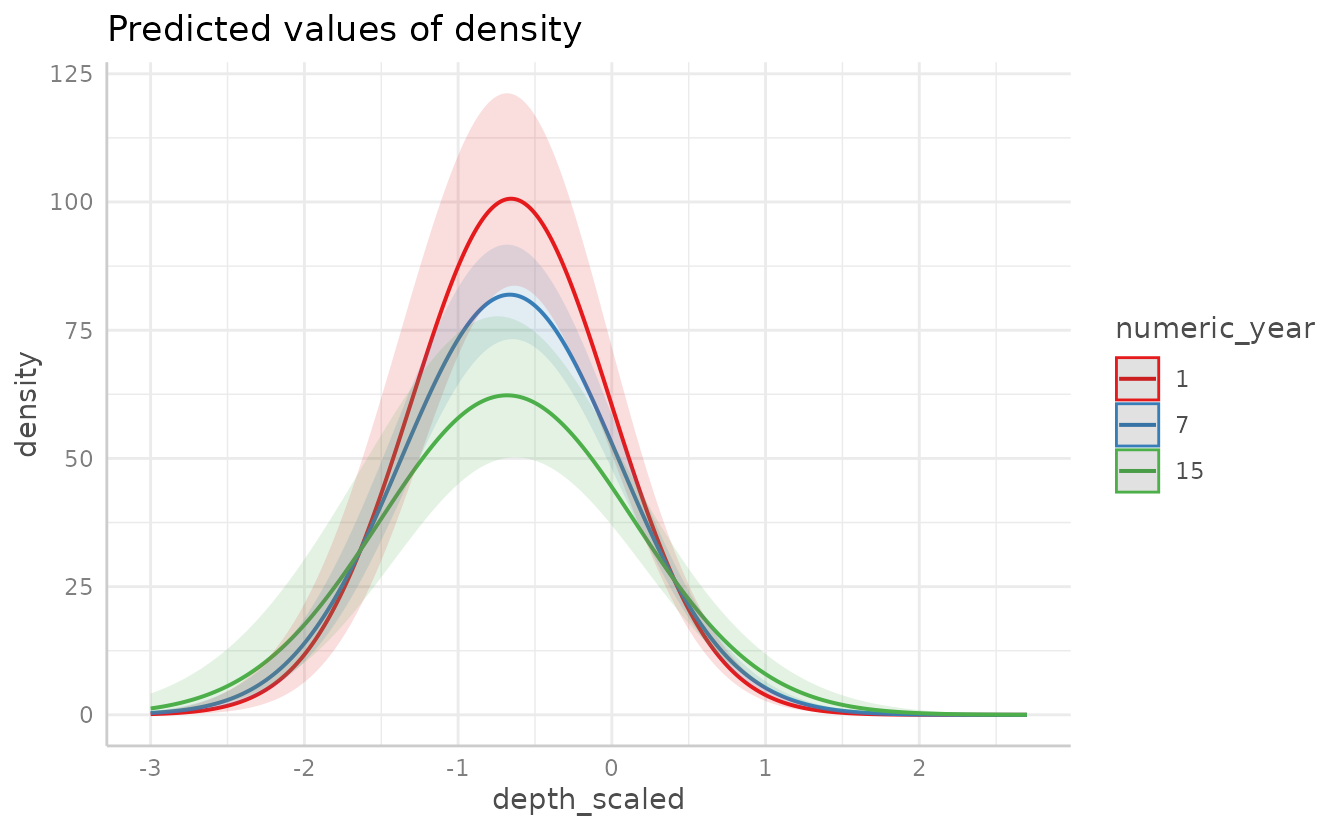
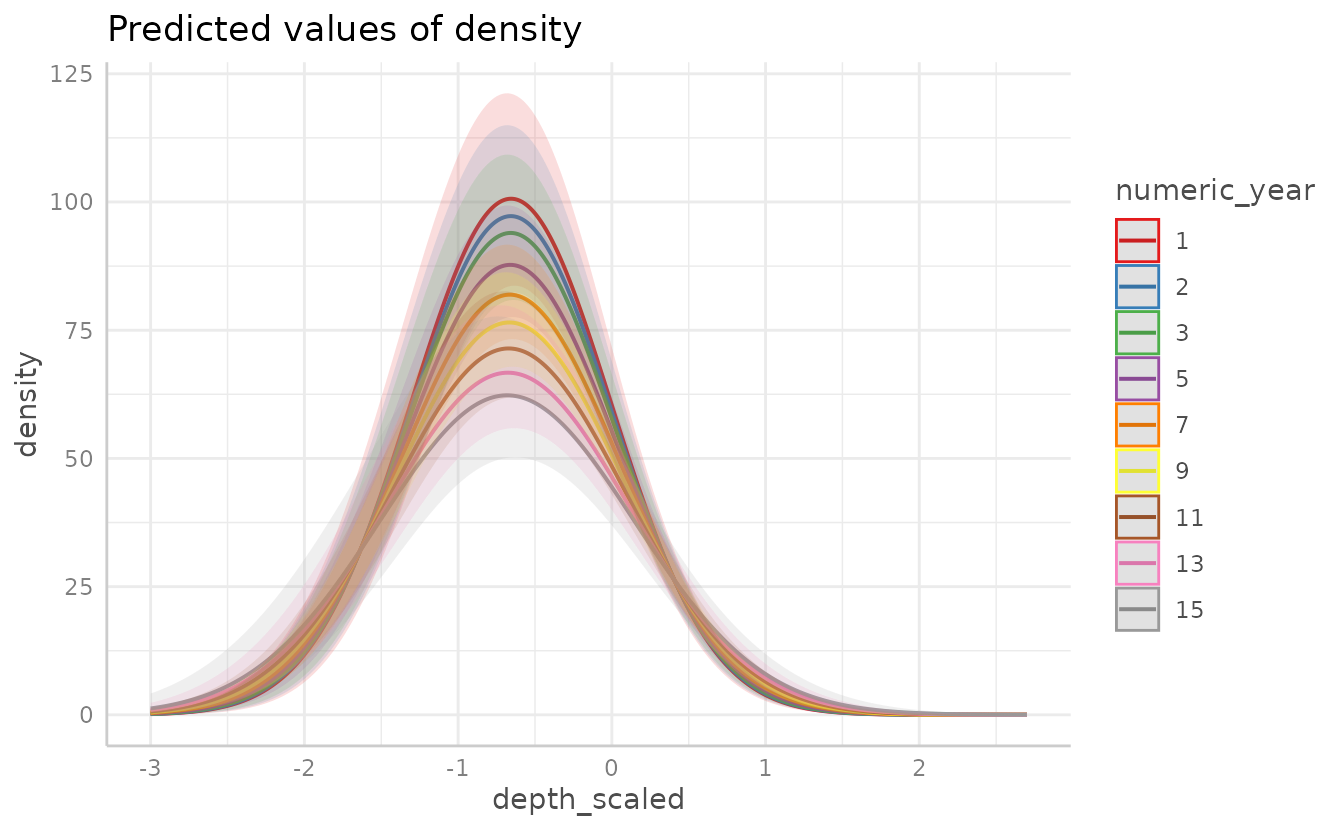
ggplot(dat, aes(x, predicted, colour = group)) +
  geom_line()

Plotting using with a continuous response (here density) rather than presence-only is similar. For instance:

We can fit a model with an interaction of two continuous variables:

For plotting two continuous variables, ggeffect() will make the non-target (2nd) variable discrete by selecting different levels.

g5 <- ggeffect(fit3, terms = c("depth_scaled [-3:2.7 by=0.01]", "numeric_year"))
plot(g5)

plot(g5, facet = TRUE)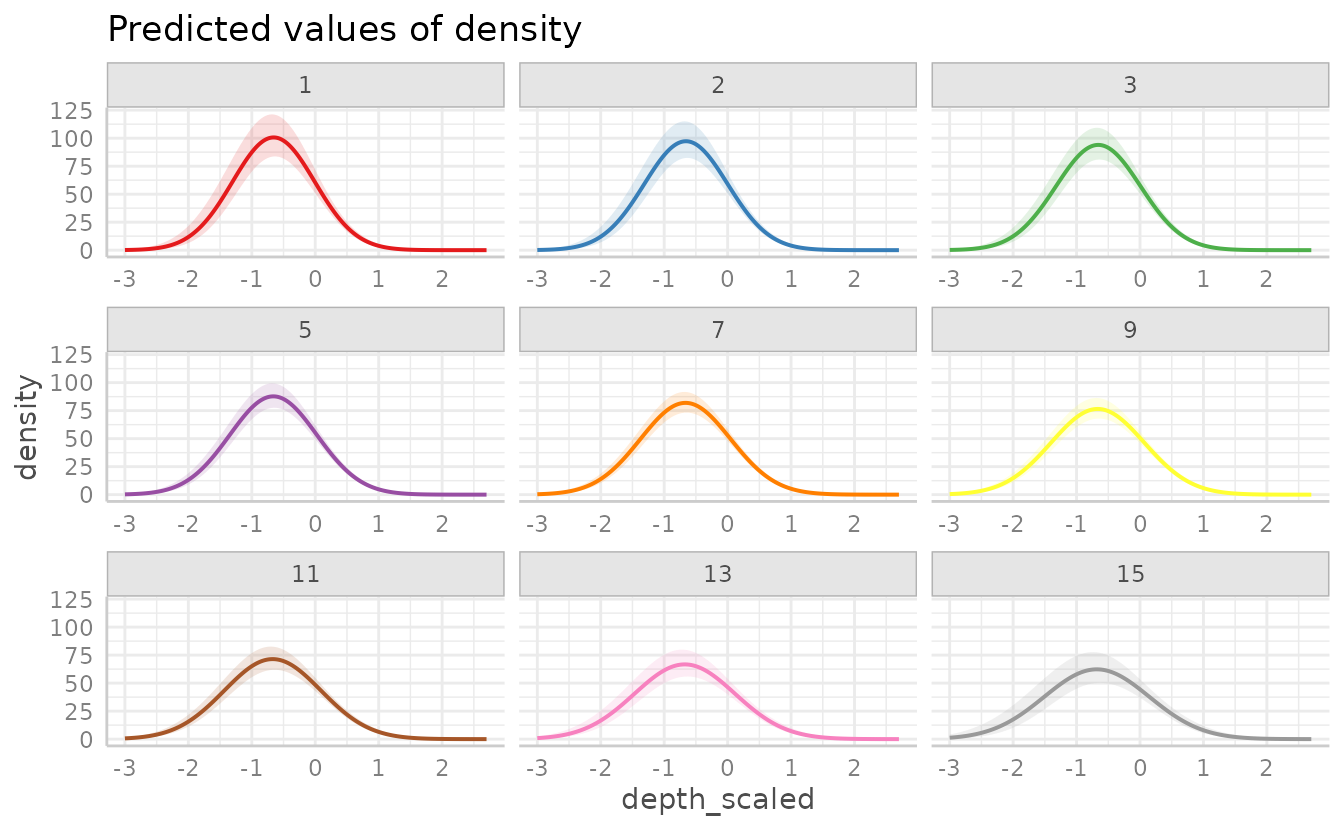

To specify the levels rather than letting ggeffect() choose them, use brackets with the selected values within the term list, for instance

g6 <- ggeffect(fit3, terms = c("depth_scaled [-3:2.7 by=0.01]", "numeric_year [1,7,15]"))
plot(g6)

Julia Indivero, Sean Anderson, Lewis Barnett, Philina English, Eric Ward

2024-07-03

Example with Pacific cod presence