Skip to contents

Index standardization with sdmTMB

2024-10-01

Source: vignettes/articles/index-standardization.Rmd
index-standardization.Rmd

If the code in this vignette has not been evaluated, a rendered version is available on the documentation site under ‘Articles’.

Let’s perform index standardization with the built-in data for Pacific cod.

  • The density units should be kg/km2.
  • Here, X and Y are coordinates in UTM zone 9.
glimpse(pcod)
#> Rows: 2,143
#> Columns: 12
#> $ year          <int> 2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003, 20…
#> $ X             <dbl> 446.4752, 446.4594, 448.5987, 436.9157, 420.6101, 417.71…
#> $ Y             <dbl> 5793.426, 5800.136, 5801.687, 5802.305, 5771.055, 5772.2…
#> $ depth         <dbl> 201, 212, 220, 197, 256, 293, 410, 387, 285, 270, 381, 1…
#> $ density       <dbl> 113.138476, 41.704922, 0.000000, 15.706138, 0.000000, 0.…
#> $ present       <dbl> 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ lat           <dbl> 52.28858, 52.34890, 52.36305, 52.36738, 52.08437, 52.094…
#> $ lon           <dbl> -129.7847, -129.7860, -129.7549, -129.9265, -130.1586, -…
#> $ depth_mean    <dbl> 5.155194, 5.155194, 5.155194, 5.155194, 5.155194, 5.1551…
#> $ depth_sd      <dbl> 0.4448783, 0.4448783, 0.4448783, 0.4448783, 0.4448783, 0…
#> $ depth_scaled  <dbl> 0.3329252, 0.4526914, 0.5359529, 0.2877417, 0.8766077, 1…
#> $ depth_scaled2 <dbl> 0.11083919, 0.20492947, 0.28724555, 0.08279527, 0.768440…

First we will create our SPDE mesh. We will use a relatively course mesh for a balance between speed and accuracy in this vignette (cutoff = 10 where cutoff is in the units of X and Y (km here) and represents the minimum distance between points before a new mesh vertex is added). You will likely want to use a higher resolution mesh for applied scenarios. You will want to make sure that increasing the number of knots does not change the conclusions.

pcod_spde <- make_mesh(pcod, c("X", "Y"), cutoff = 10)
plot(pcod_spde)

Let’s fit a GLMM. Note that if you want to use this model for index standardization then you will likely want to include 0 + as.factor(year) or -1 + as.factor(year) so that there is a factor predictor that represents the mean estimate for each time slice.

m <- sdmTMB(
  data = pcod, 
  formula = density ~ 0 + as.factor(year),
  time = "year", mesh = pcod_spde, family = tweedie(link = "log"))

We can inspect randomized quantile residuals:

pcod$resids <- residuals(m) # randomized quantile residuals
#> Note what used to be the default sdmTMB residuals (before version 0.4.3.9005)
#> are now `type = 'mle-eb'`. We recommend using the current default `'mle-mvn'`,
#> which takes one sample from the approximate posterior of the random effects or
#> `dharma_residuals()` using a similar approach.
# Also see residuals(..., type = "mle-mcmc") which are better but slower
hist(pcod$resids)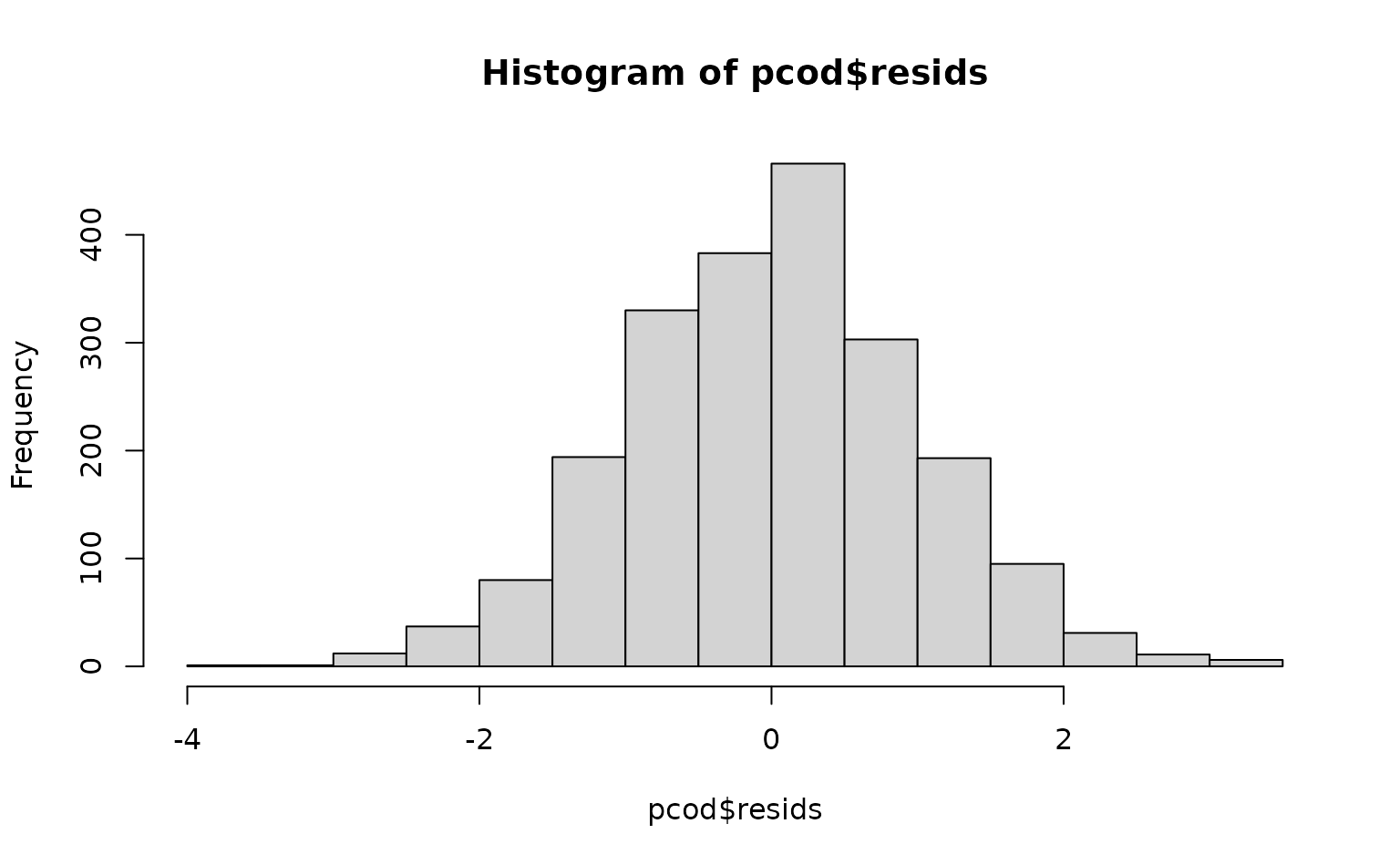

qqnorm(pcod$resids)
abline(a = 0, b = 1)

ggplot(pcod, aes(X, Y, col = resids)) + scale_colour_gradient2() +
  geom_point() + facet_wrap(~year) + coord_fixed()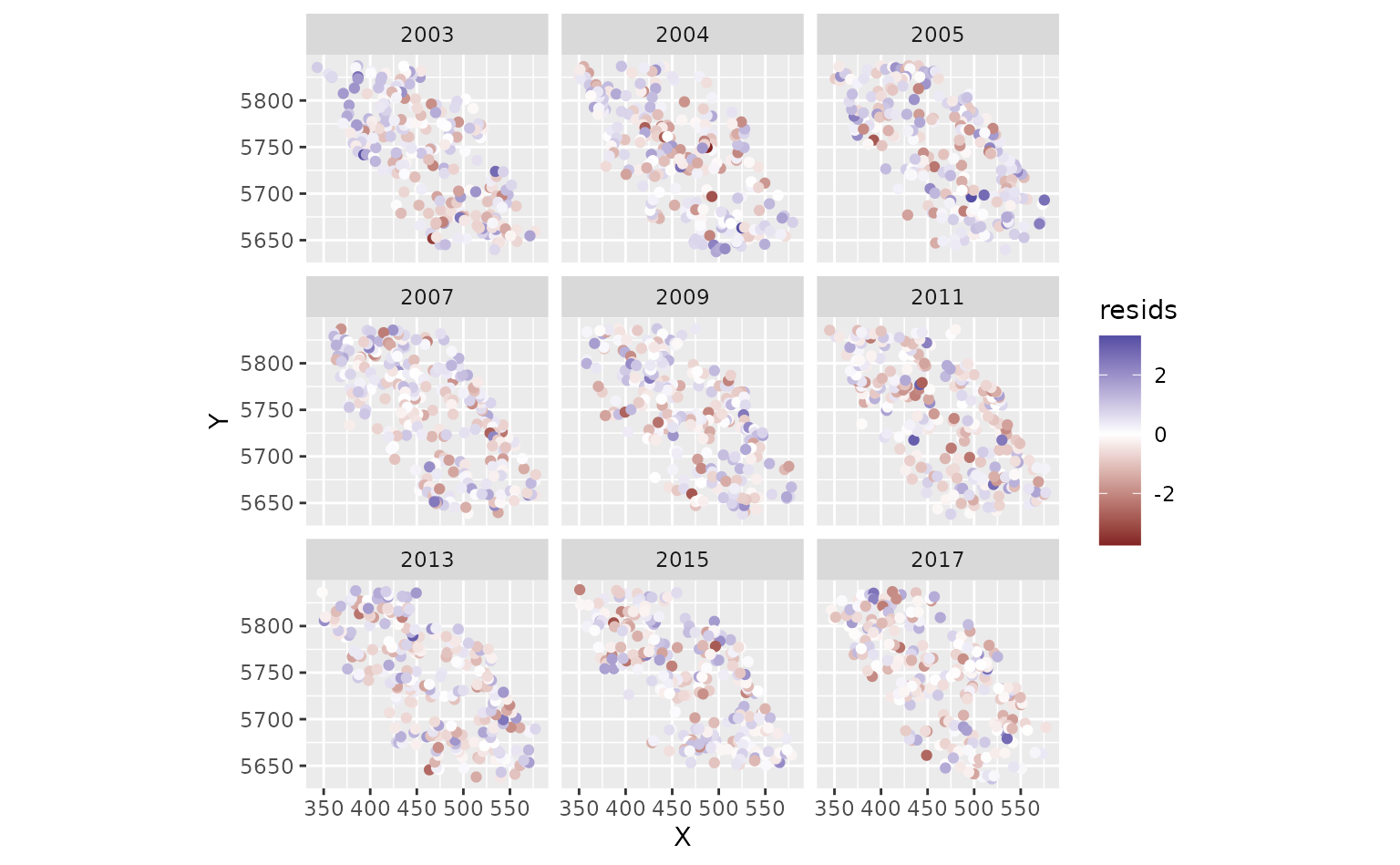

Now we want to predict on a fine-scale grid on the entire survey domain. There is a grid built into the package for Queen Charlotte Sound named qcs_grid. Our prediction grid also needs to have all the covariates that we used in the model above.

glimpse(qcs_grid)
#> Rows: 7,314
#> Columns: 5
#> $ X             <dbl> 456, 458, 460, 462, 464, 466, 468, 470, 472, 474, 476, 4…
#> $ Y             <dbl> 5636, 5636, 5636, 5636, 5636, 5636, 5636, 5636, 5636, 56…
#> $ depth         <dbl> 347.08345, 223.33479, 203.74085, 183.29868, 182.99983, 1…
#> $ depth_scaled  <dbl> 1.56081222, 0.56976988, 0.36336929, 0.12570465, 0.122036…
#> $ depth_scaled2 <dbl> 2.436134794, 0.324637712, 0.132037240, 0.015801659, 0.01…

We can replicate our grid across all years:

grid_yrs <- replicate_df(qcs_grid, "year", unique(pcod$year))

Now make the predictions on new data.

predictions <- predict(m, newdata = grid_yrs, return_tmb_object = TRUE)

Let’s make a small function to make maps.

plot_map <- function(dat, column) {
  ggplot(dat, aes(X, Y, fill = {{ column }})) +
    geom_raster() +
    facet_wrap(~year) +
    coord_fixed()
}

There are four kinds of predictions that we get out of the model. First we will show the predictions that incorporate all fixed effects and random effects:

plot_map(predictions$data, exp(est)) +
  scale_fill_viridis_c(trans = "sqrt") +
  ggtitle("Prediction (fixed effects + all random effects)")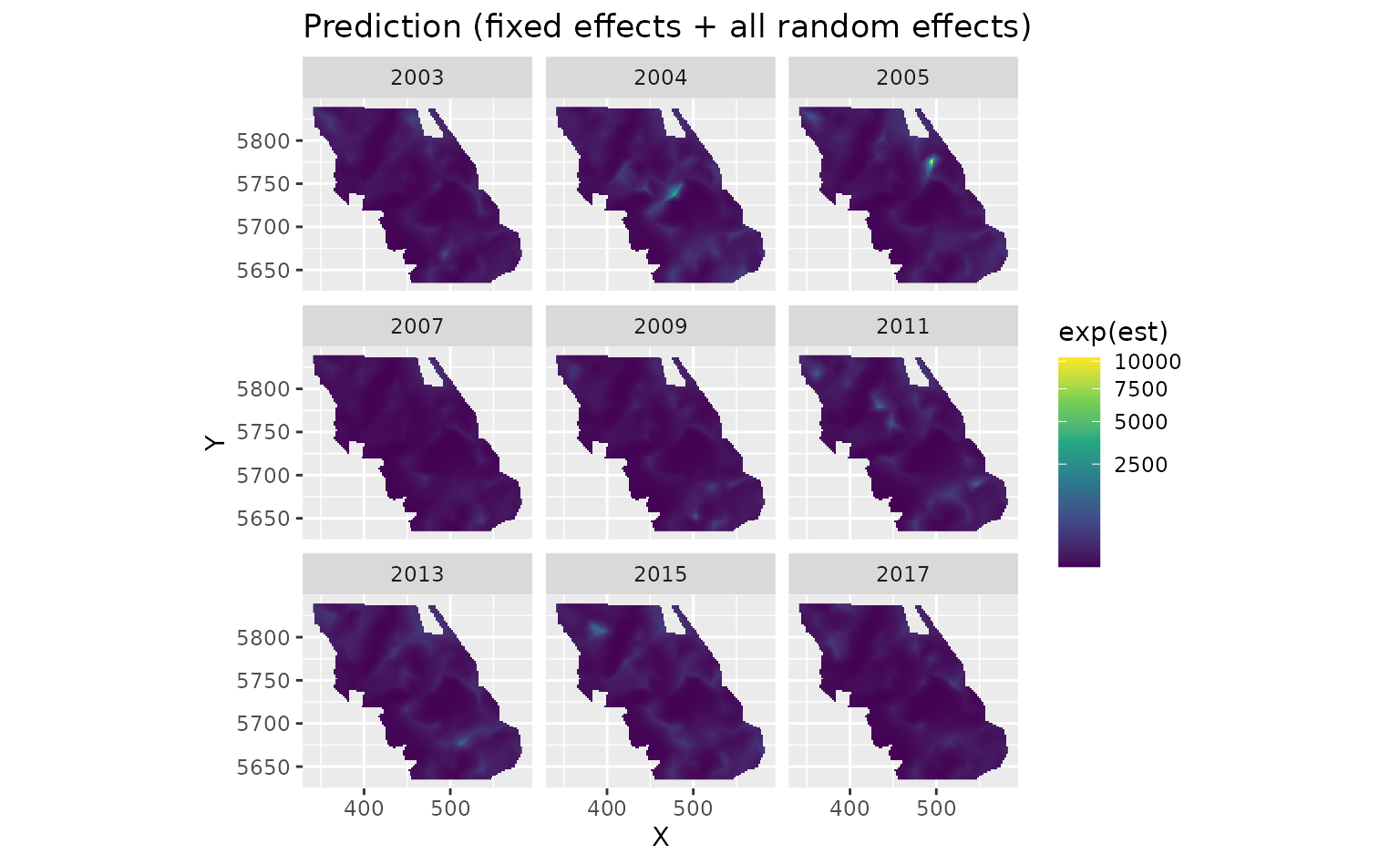

We can also look at just the fixed effects, here year:

plot_map(predictions$data, exp(est_non_rf)) +
  ggtitle("Prediction (fixed effects only)") +
  scale_fill_viridis_c(trans = "sqrt")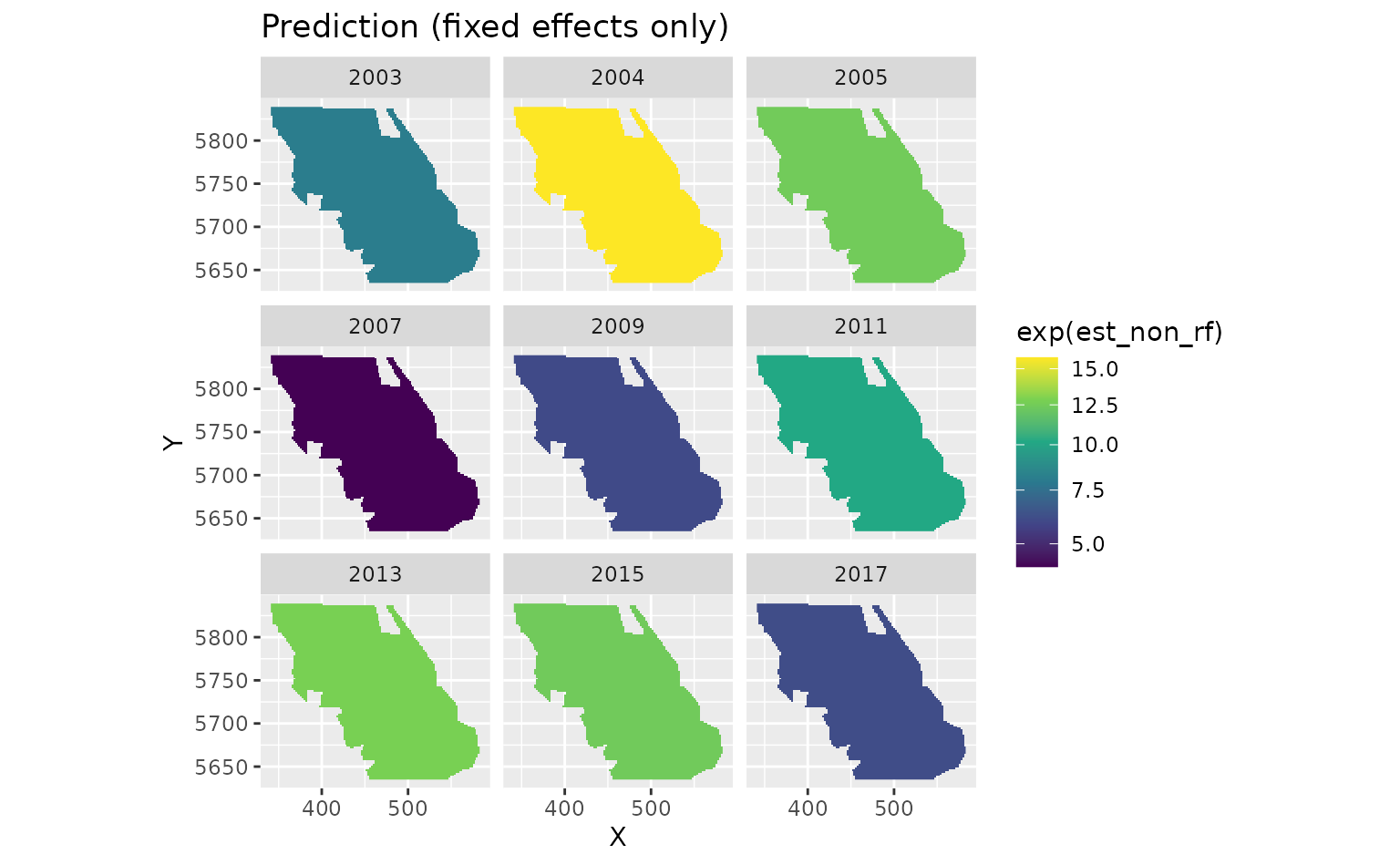

We can look at the spatial random effects that represent consistent deviations in space through time that are not accounted for by our fixed effects. In other words, these deviations represent consistent biotic and abiotic factors that are affecting biomass density but are not accounted for in the model.

plot_map(predictions$data, omega_s) +
  ggtitle("Spatial random effects only") +
  scale_fill_gradient2()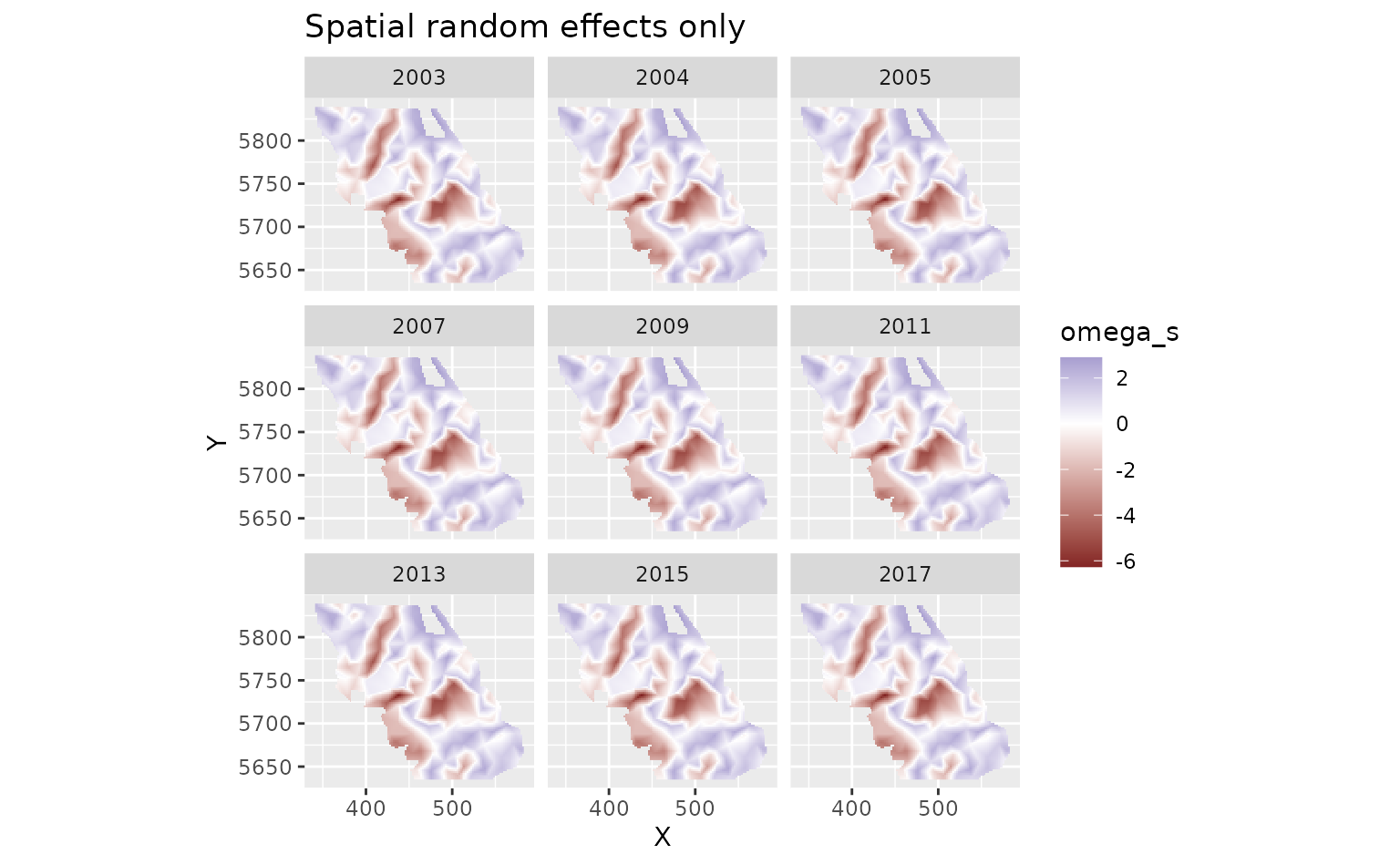

And finally we can look at the spatiotemporal random effects that represent deviation from the fixed effect predictions and the spatial random effect deviations. These represent biotic and abiotic factors that are changing through time and are not accounted for in the model.

plot_map(predictions$data, epsilon_st) +
  ggtitle("Spatiotemporal random effects only") +
  scale_fill_gradient2()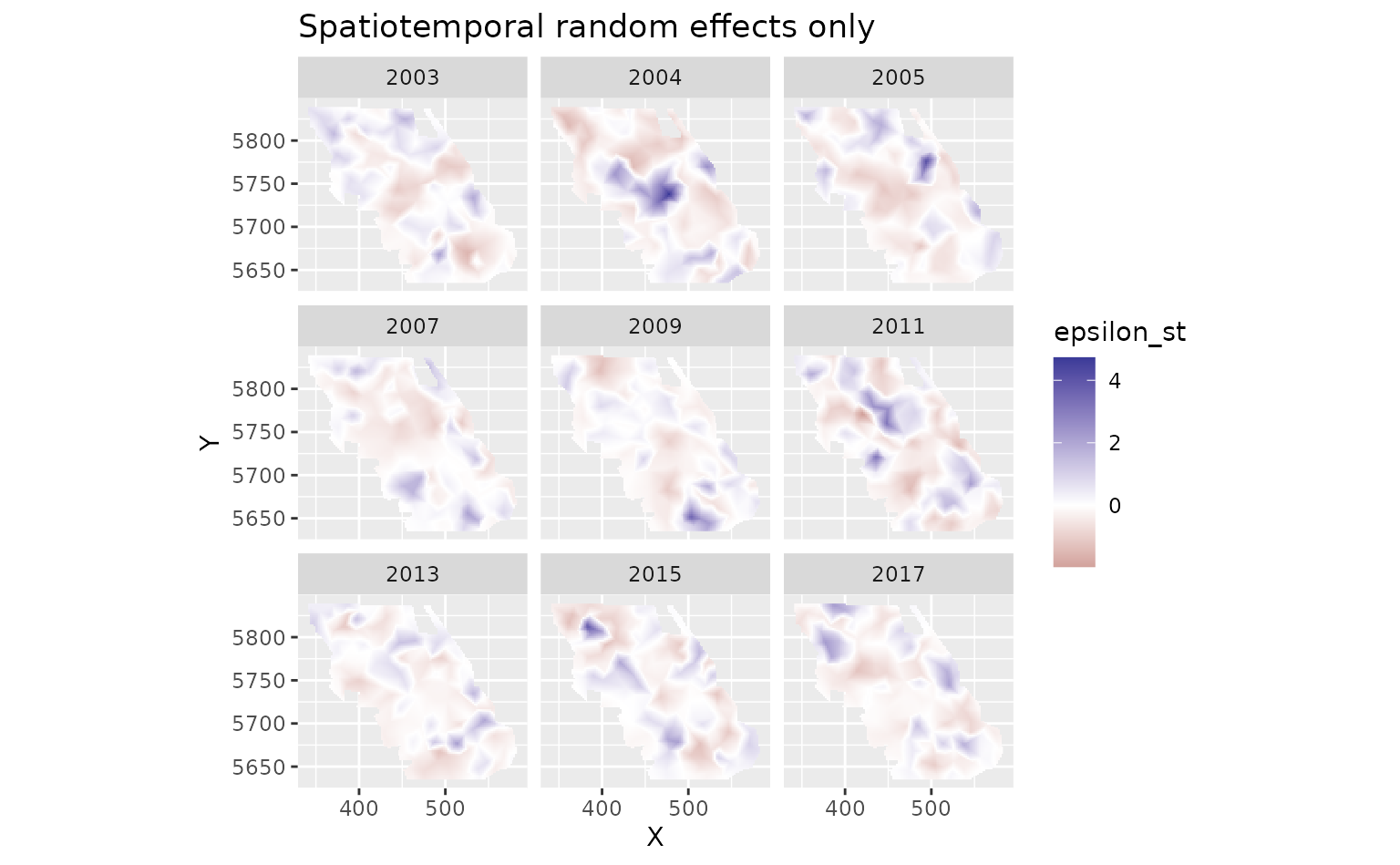

When we ran our predict.sdmTBM() function, it also returned a report from TMB in the output because we included return_tmb_object = TRUE. We can then run our get_index() function to extract the total biomass calculations and standard errors.

We will need to set the area argument to 4 km2 since our grid cells are 2 km x 2 km. If some grid cells were not fully in the survey domain (or were on land), we could feed a vector of grid areas to the area argument that matched the number of grid cells.

index <- get_index(predictions, area = 4, bias_correct = TRUE)
ggplot(index, aes(year, est)) + geom_line() +
  geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.4) +
  xlab('Year') + ylab('Biomass estimate (kg)')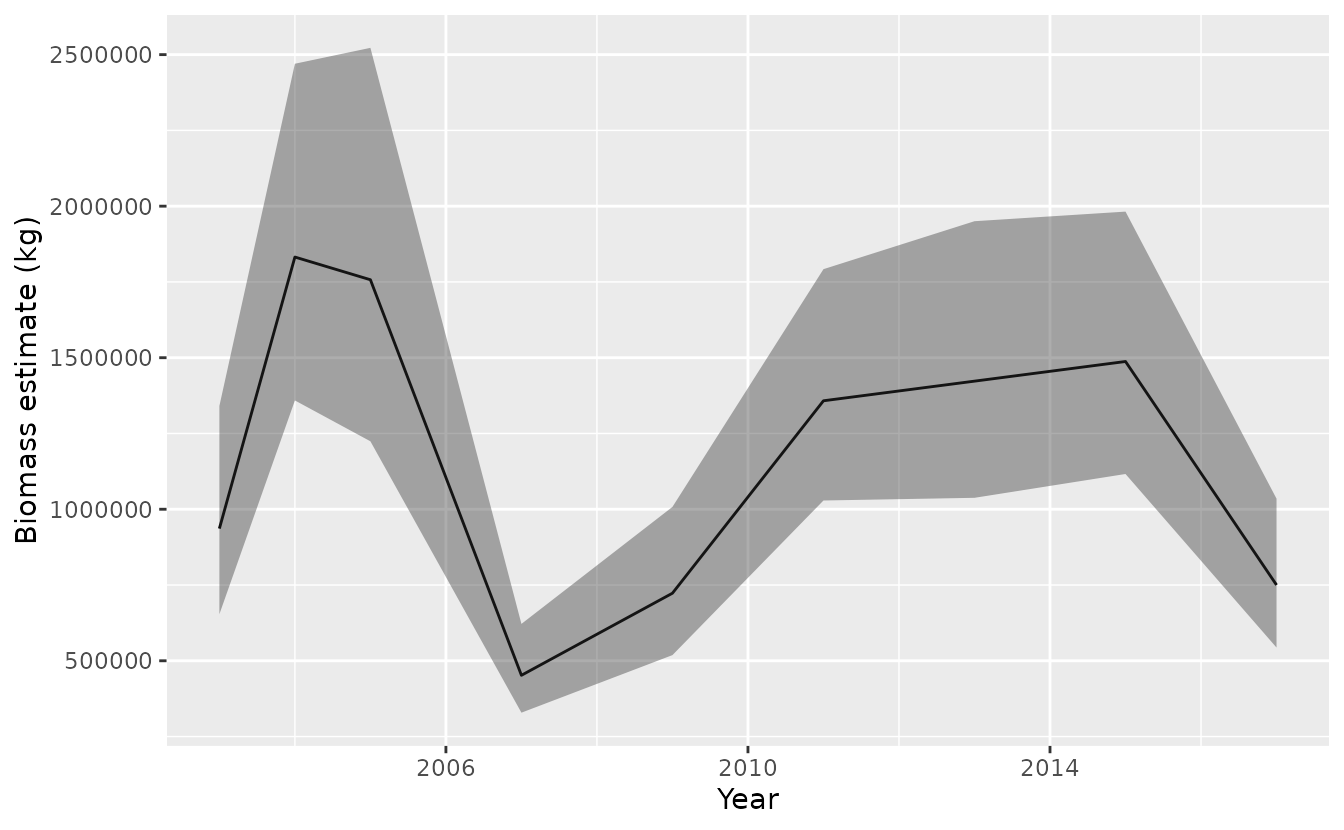

These are our biomass estimates:

mutate(index, cv = sqrt(exp(se^2) - 1)) %>% 
  select(-log_est, -se) %>%
  knitr::kable(format = "pandoc", digits = c(0, 0, 0, 0, 2))
year est lwr upr type cv
2003 936176 653699 1340716 index 0
2004 1832130 1359020 2469943 index 0
2005 1757227 1224189 2522360 index 0
2007 452112 328786 621698 index 0
2009 722982 518713 1007692 index 0
2011 1357885 1028851 1792147 index 0
2013 1422648 1037721 1950358 index 0
2015 1487473 1116301 1982062 index 0
2017 750051 543622 1034867 index 0

We can also calculate an index for part of the survey domain. We’ll make an index for everything south of UTM 5700 by subsetting our prediction grid. For more complicated spatial polygons you could intersect the polygon on the prediction grid using something like sf::st_intersects().

qcs_grid_south <- grid_yrs[grid_yrs$Y < 5700, ]
predictions_south <- predict(m, newdata = qcs_grid_south, 
  return_tmb_object = TRUE)
index_south <- get_index(predictions_south, area = 4, bias_correct = TRUE)
head(index_south)
#>   year      est      lwr      upr  log_est        se  type
#> 1 2003 264679.9 156368.9 448013.9 12.48628 0.2685270 index
#> 2 2004 602466.8 403037.0 900577.8 13.30879 0.2051079 index
#> 3 2005 411739.0 263138.9 644256.8 12.92814 0.2284265 index
#> 4 2007 184945.7 117598.4 290861.9 12.12782 0.2310178 index
#> 5 2009 316483.8 203600.9 491952.5 12.66503 0.2250603 index
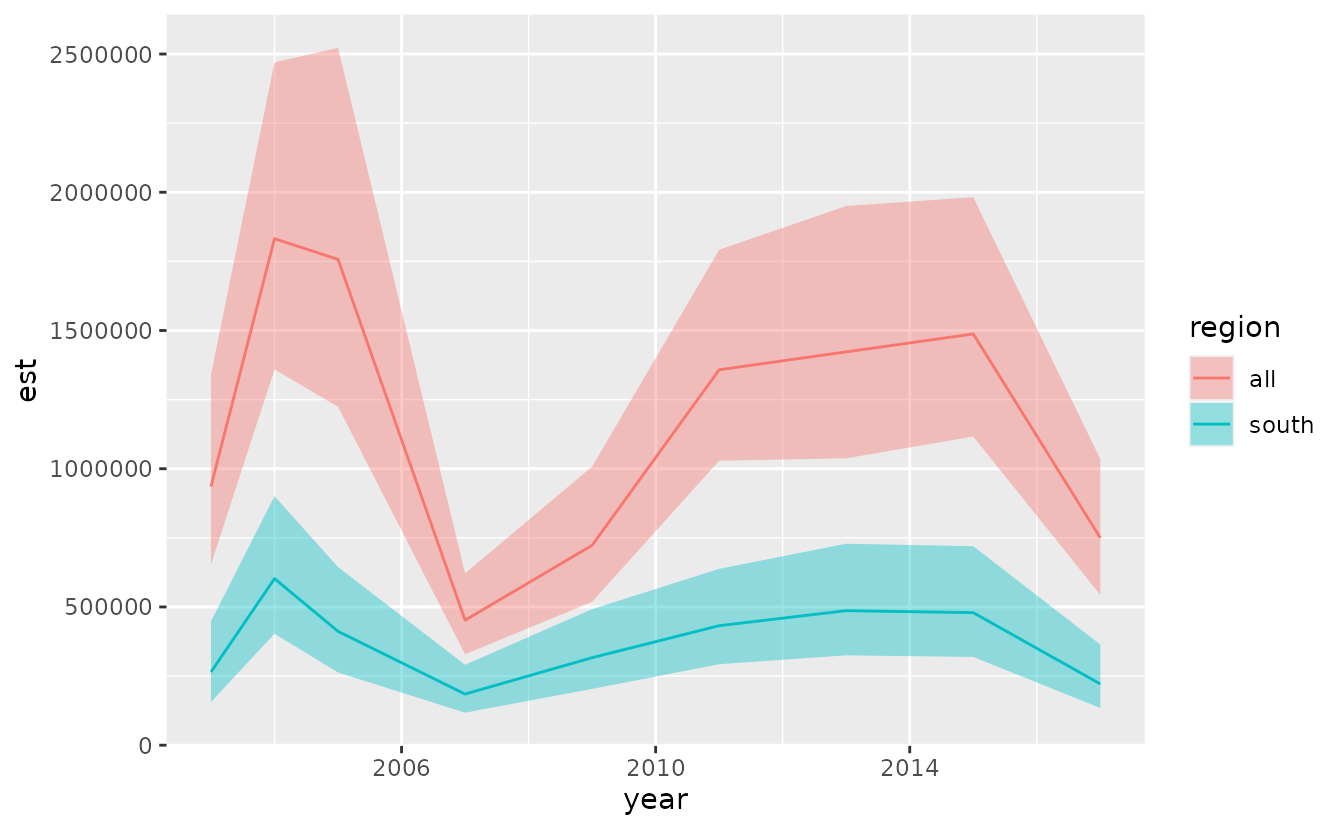
#> 6 2011 432243.6 292909.8 637857.0 12.97674 0.1985366 index

We can visually compare the two indexes:

mutate(index, region = "all") %>% 
  bind_rows(mutate(index_south, region = "south")) %>% 
  ggplot(aes(year, est)) + 
  geom_line(aes(colour = region)) +
  geom_ribbon(aes(ymin = lwr, ymax = upr, fill = region), alpha = 0.4)