Fitting delta (hurdle) models with sdmTMB

If the code in this vignette has not been evaluated, a rendered version is available on the documentation site under ‘Articles’.

library(ggplot2)
library(dplyr)
library(sdmTMB)

sdmTMB has the capability for built-in hurdle models (also called delta models). These are models with one model for zero vs. non-zero data and another component for the positive component. Hurdle models could also be implemented by fitting the two components separately and combining the predictions.

Hurdle models are more appropriate than something like a Tweedie when there are differences in the processes controlling presence vs. abundance, or when greater flexibility to account for dispersion is required.

Built-in hurdle models can be specified with the family argument within the sdmTMB() function. Current options include:

Delta-Gamma: family = delta_gamma(link1 = "logit", link2 = "log"). This fits a binomial presence-absence model (i.e., binomial(link = "logit")) and then a model for the positive catches only with a Gamma observation distribution and a log link (i.e., Gamma(link = "log")). Here and with other delta models, the link1 and link2 can be omitted and left at their default values.
Delta-lognormal: family = delta_lognormal(). This fits a binomial presence-absence model (i.e., binomial(link = "logit")) and then a model for the positive catches only with a lognormal observation distribution and a log link (i.e., lognormal(link = "log")
Poisson-link delta-Gamma or delta-lognormal. See the Poisson-link delta model vignette.
Delta-truncated-negative-binomial: family = delta_truncated_nbinom1() or family = delta_truncated_nbinom2(). This fits a binomial presence-absence model (binomial(link = "logit")) and a truncated_nbinom1(link = "log") or truncated_nbinom1(link = "log") distribution for positive catches.

To summarize the built-in delta models and the separate components:

Model Type	Built-in delta function	Presence-absence model	Positive catch model
Delta-gamma	`delta_gamma()`	`binomial(link = "logit")`	`Gamma(link = "log")`
Delta-lognormal	`delta_lognormal()`	`binomial(link = "logit")`	`lognormal(link = "log")`
Delta-NB1	`delta_truncated_nbinom1()`	`binomial(link = "logit")`	`truncated_nbinom1(link = "log")`
Delta-NB2	`delta_truncated_nbinom2()`	`binomial(link = "logit")`	`truncated_nbinom2(link = "log")`

Example with built-in delta model

Here, we will show an example of fitting using the built-in delta functionality, as well as how to build each model component separately and then combine. The built-in approach is convenient, allows for parameters to be shared across components, and allows for calculation of derived quantities such as standardized indexes (get_index()) with internally calculated standard errors.

We will use a dataset built into the sdmTMB package: trawl survey data for Pacific Cod in Queen Charlotte Sound, British Columbia, Canada. The density units are kg/km². Here, X and Y are coordinates in UTM zone 9.

We will first create a mesh that we will use for all the models.

pcod_mesh <- make_mesh(pcod, c("X", "Y"), cutoff = 15)

Then we can fit a model of Pacific cod density using a delta-gamma model, including a smoothed effect of depth.

fit_dg <- sdmTMB(density ~ 1 + s(depth),
  data = pcod,
  mesh = pcod_mesh,
  time = "year",
  family = delta_gamma()
)

The default in built-in delta models is for the formula, spatial and spatiotemporal structure, and anisotropy to be shared between the two model components. However, some elements (formula, spatial, spatiotemporal, and share_range) can also be specified independently for each model using a list format within the function argument (see examples below). The first element of the list is for the binomial component and the second element is for the positive component (e.g., Gamma). Some elements must be shared for now (e.g., smoothers, spatially varying coefficients, and time-varying coefficients).

To specify the settings for spatial and spatiotemporal effects in each model component, create a list of settings within the spatial and spatiotemporal arguments. For example, spatial = list("on", "off"), spatiotemporal = list("off", "rw").

We could similarly specify a different formula for each component of the model, using list(y ~ x1, y ~ x2) For instance, we could include the effect of depth for only the positive model, and remove it for the presence-absence model.

However, there are currently limitations if specifying separate formulas for each model component. The two formulas cannot have:

smoothers
threshold effects
random intercepts

For now, these must be specified through a single formula that is shared across the two models.

Each model component can similarly have separate settings for share_range, which determines whether there is a shared spatial and spatiotemporal range parameter (TRUE) or independent range parameters (FALSE), by using a list.

Lastly, whether or not anisotropy is included in the model is determined with the logical argument anisotropy (i.e., TRUE or FALSE), and cannot be separately specified for each model. If anisotropy is included, it is by default shared across the two model components. However it can be made unique in each model component by using sdmTMBcontrol(map = ...) and adding the argument control when fitting the model. This ‘maps’ the anisotropy parameters be unique across model components.

Once we fit the delta model, we can evaluate and plot the output, diagnostics, and predictions similar to other sdmTMB models.

The printed model output will show estimates and standard errors of parameters for each model separately.

print(fit_dg)
#> Spatiotemporal model fit by ML ['sdmTMB']
#> Formula: density ~ 1 + s(depth)
#> Mesh: pcod_mesh (isotropic covariance)
#> Time column: year
#> Data: pcod
#> Family: delta_gamma(link1 = 'logit', link2 = 'log')
#> 
#> Delta/hurdle model 1: -----------------------------------
#> Family: binomial(link = 'logit') 
#>             coef.est coef.se
#> (Intercept)    -0.34    0.61
#> sdepth          1.28    2.91
#> 
#> Smooth terms:
#>            Std. Dev.
#> sds(depth)     14.38
#> 
#> Matérn range: 61.41
#> Spatial SD: 1.71
#> Spatiotemporal IID SD: 0.81
#> 
#> Delta/hurdle model 2: -----------------------------------
#> Family: Gamma(link = 'log') 
#>             coef.est coef.se
#> (Intercept)     3.67    0.12
#> sdepth          0.31    1.29
#> 
#> Smooth terms:
#>            Std. Dev.
#> sds(depth)      5.41
#> 
#> Dispersion parameter: 1.03
#> Matérn range: 14.80
#> Spatial SD: 0.69
#> Spatiotemporal IID SD: 1.45
#> 
#> ML criterion at convergence: 6126.400
#> 
#> See ?tidy.sdmTMB to extract these values as a data frame.

Using the tidy() function will turn the sdmTMB model output into a data frame, with the argument model=1 or model=2 to specify which model component to extract as a dataframe. See tidy.sdmTMB() for additional arguments and options.

tidy(fit_dg) # model = 1 is default
#> # A tibble: 1 × 5
#>   term        estimate std.error conf.low conf.high
#>   <chr>          <dbl>     <dbl>    <dbl>     <dbl>
#> 1 (Intercept)   -0.343     0.614    -1.55     0.860
tidy(fit_dg, model = 1)
#> # A tibble: 1 × 5
#>   term        estimate std.error conf.low conf.high
#>   <chr>          <dbl>     <dbl>    <dbl>     <dbl>
#> 1 (Intercept)   -0.343     0.614    -1.55     0.860
tidy(fit_dg, model = 1, "ran_pars", conf.int = TRUE)
#> # A tibble: 3 × 5
#>   term    estimate std.error conf.low conf.high
#>   <chr>      <dbl>     <dbl>    <dbl>     <dbl>
#> 1 range     61.4      14.1     39.2       96.3 
#> 2 sigma_O    1.71      0.265    1.26       2.32
#> 3 sigma_E    0.806     0.142    0.570      1.14
tidy(fit_dg, model = 2)
#> # A tibble: 1 × 5
#>   term        estimate std.error conf.low conf.high
#>   <chr>          <dbl>     <dbl>    <dbl>     <dbl>
#> 1 (Intercept)     3.67     0.120     3.44      3.91
tidy(fit_dg, model = 2, "ran_pars", conf.int = TRUE)
#> # A tibble: 4 × 5
#>   term    estimate std.error conf.low conf.high
#>   <chr>      <dbl>     <dbl>    <dbl>     <dbl>
#> 1 range     14.8      5.02      7.62      28.8 
#> 2 phi        1.03     0.0502    0.939      1.14
#> 3 sigma_O    0.691    0.228     0.361      1.32
#> 4 sigma_E    1.45     0.336     0.919      2.28

For built-in delta models, the default function will return estimated response and parameters for each grid cell for each model separately, notated with a 1 (for the presence/absence model) or 2 (for the positive catch model) in the column name. See predict.sdmTMB() for a description of values in the data frame.

grid_yrs <- replicate_df(qcs_grid, "year", unique(pcod$year))
p <- predict(fit_dg, newdata = grid_yrs)
str(p)
#> 'data.frame':    65826 obs. of  16 variables:
#>  $ X            : num  456 458 460 462 464 466 468 470 472 474 ...
#>  $ Y            : num  5636 5636 5636 5636 5636 ...
#>  $ depth        : num  347 223 204 183 183 ...
#>  $ depth_scaled : num  1.561 0.57 0.363 0.126 0.122 ...
#>  $ depth_scaled2: num  2.4361 0.3246 0.132 0.0158 0.0149 ...
#>  $ year         : int  2003 2003 2003 2003 2003 2003 2003 2003 2003 2003 ...
#>  $ est1         : num  -5.804 -0.796 0.021 0.87 0.98 ...
#>  $ est2         : num  3.2 3.71 4.02 4.39 4.43 ...
#>  $ est_non_rf1  : num  -5.508 -0.598 0.12 0.871 0.882 ...
#>  $ est_non_rf2  : num  2.83 3.31 3.59 3.94 3.94 ...
#>  $ est_rf1      : num  -0.296138 -0.197484 -0.09883 -0.000177 0.098477 ...
#>  $ est_rf2      : num  0.368 0.398 0.428 0.459 0.489 ...
#>  $ omega_s1     : num  -0.00543 0.09317 0.19178 0.29039 0.38899 ...
#>  $ omega_s2     : num  0.108 0.119 0.129 0.139 0.15 ...
#>  $ epsilon_st1  : num  -0.291 -0.291 -0.291 -0.291 -0.291 ...
#>  $ epsilon_st2  : num  0.26 0.28 0.299 0.319 0.339 ...

We can use predictions from the built-in delta model (making sure that return_tmb_object=TRUE) to get the index values using the get_index() function. This can be used with predictions that include both the first and second models (i.e., using the default and specifying no model argument) or with predictions generated using model=NA. The get_index() function will automatically combine predictions from the first and second model in calculating the index values. For more on modelling for the purposes of creating an index see the vignette on Index standardization with sdmTMB.

p2 <- predict(fit_dg, newdata = grid_yrs, return_tmb_object = TRUE)
ind_dg <- get_index(p2, bias_correct = FALSE)

We can plot conditional effects of covariates (such as depth in the example model) using the package visreg by specifying each model component with model=1 for the presence-absence model or model=2 for the positive catch model. Currently, plotting effects of built-in delta models with ggeffects is not supported. See the vignette on using visreg with sdmTMB for more information.

visreg_delta(fit_dg, xvar = "depth", model = 1, gg = TRUE)
#> These are residuals for delta model component 1. Use the `model` argument to
#> select the other component.

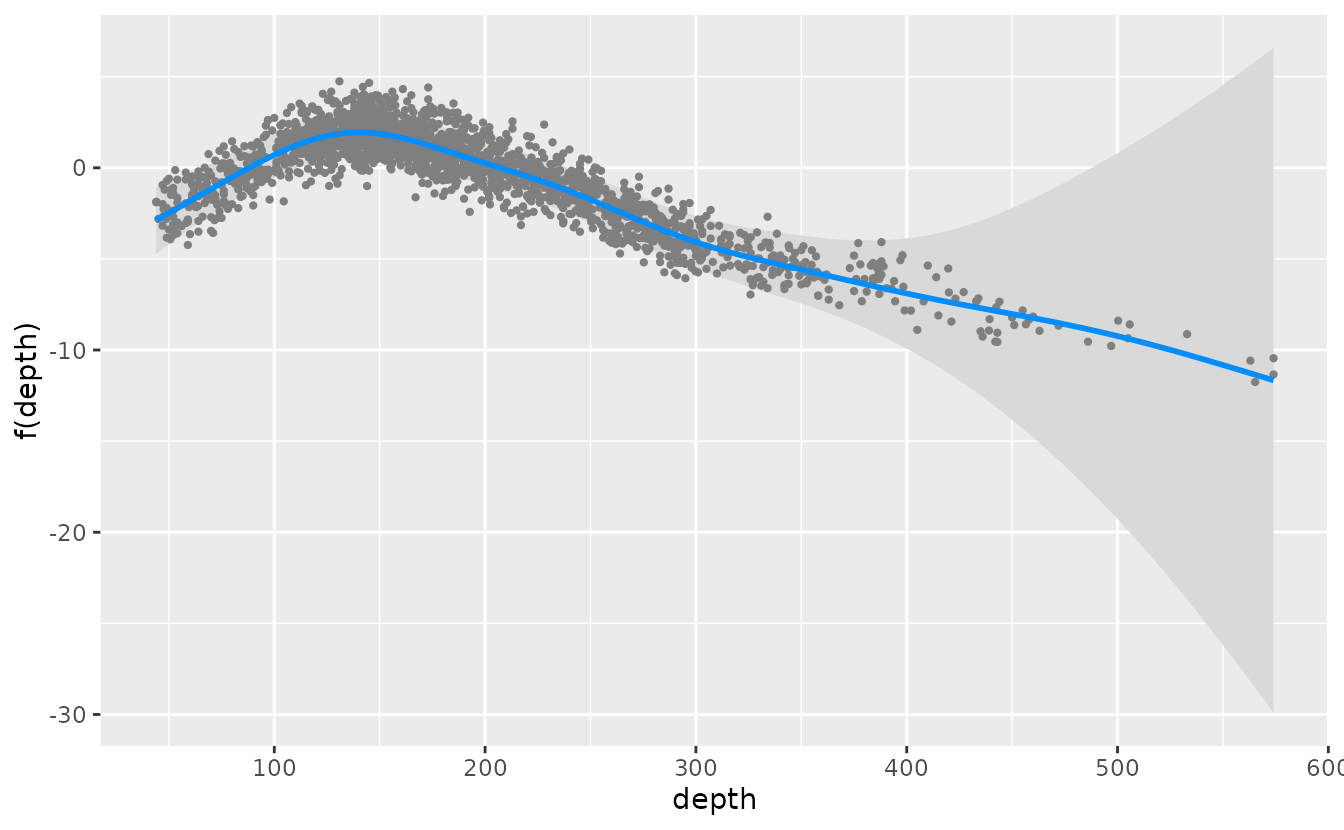
visreg_delta(fit_dg, xvar = "depth", model = 2, gg = TRUE)

The built-in delta models can also be evaluated with the residuals() functions in sdmTMB. Similarly to generating predictions, we can specify which of the model components we want to return residuals for using the model argument and specifying =1 or =2. See residuals.sdmTMB() for additional options for evaluating residuals in sdmTMB models.

We can also simulate new observations from a fitted delta model. As in other functions, we can specify which model to simulate from using the argument model=1 for only presence/absence, model=2 for only positive catches, or model=NA for combined predictions. See simulate.sdmTMB() for more details on simulation options.

simulations <- simulate(fit_dg, nsim = 5, seed = 5090, model = NA)

Delta models by fitting two components separately and combining predictions

Next, we will show an example of how to implement a delta-gamma model in sdmTMB, but with each component fit separately and then combined. This approach gives maximum flexibility for each model and lets you develop them on at a time. It has limitations if you are calculating an index of abundance or if you want to share some parameters.

glimpse(pcod)
#> Rows: 2,143
#> Columns: 12
#> $ year          <int> 2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003, 20…
#> $ X             <dbl> 446.4752, 446.4594, 448.5987, 436.9157, 420.6101, 417.71…
#> $ Y             <dbl> 5793.426, 5800.136, 5801.687, 5802.305, 5771.055, 5772.2…
#> $ depth         <dbl> 201, 212, 220, 197, 256, 293, 410, 387, 285, 270, 381, 1…
#> $ density       <dbl> 113.138476, 41.704922, 0.000000, 15.706138, 0.000000, 0.…
#> $ present       <dbl> 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ lat           <dbl> 52.28858, 52.34890, 52.36305, 52.36738, 52.08437, 52.094…
#> $ lon           <dbl> -129.7847, -129.7860, -129.7549, -129.9265, -130.1586, -…
#> $ depth_mean    <dbl> 5.155194, 5.155194, 5.155194, 5.155194, 5.155194, 5.1551…
#> $ depth_sd      <dbl> 0.4448783, 0.4448783, 0.4448783, 0.4448783, 0.4448783, 0…
#> $ depth_scaled  <dbl> 0.3329252, 0.4526914, 0.5359529, 0.2877417, 0.8766077, 1…
#> $ depth_scaled2 <dbl> 0.11083919, 0.20492947, 0.28724555, 0.08279527, 0.768440…

mesh1 <- make_mesh(pcod, c("X", "Y"), cutoff = 20) # coarse for vignette speed

It is not necessary to use the same mesh for both models, but one can do so by updating the first mesh to match the reduced data frame as shown here:

dat2 <- subset(pcod, density > 0)
mesh2 <- make_mesh(dat2,
  xy_cols = c("X", "Y"),
  mesh = mesh1$mesh
)

This delta-gamma model is similar to the Tweedie model in the Intro to modelling with sdmTMB vignette, except that we will use s() for the depth effect.

m1 <- sdmTMB(
  formula = present ~ 0 + as.factor(year) + s(depth, k = 3),
  data = pcod,
  mesh = mesh1,
  time = "year", family = binomial(link = "logit"),
  spatiotemporal = "iid",
  spatial = "on"
)
m1
#> Spatiotemporal model fit by ML ['sdmTMB']
#> Formula: present ~ 0 + as.factor(year) + s(depth, k = 3)
#> Mesh: mesh1 (isotropic covariance)
#> Time column: year
#> Data: pcod
#> Family: binomial(link = 'logit')
#>  
#>                     coef.est coef.se
#> as.factor(year)2003    -0.76    0.42
#> as.factor(year)2004    -0.40    0.42
#> as.factor(year)2005    -0.42    0.42
#> as.factor(year)2007    -1.40    0.42
#> as.factor(year)2009    -1.16    0.42
#> as.factor(year)2011    -1.56    0.42
#> as.factor(year)2013    -0.38    0.42
#> as.factor(year)2015    -0.65    0.42
#> as.factor(year)2017    -1.56    0.42
#> sdepth                 -5.66    0.50
#> 
#> Smooth terms:
#>            Std. Dev.
#> sds(depth)      85.9
#> 
#> Matérn range: 28.70
#> Spatial SD: 1.89
#> Spatiotemporal IID SD: 0.90
#> ML criterion at convergence: 1054.414
#> 
#> See ?tidy.sdmTMB to extract these values as a data frame.

One can use different covariates in each model, but in this case we will just let the depth effect be more wiggly by not specifying k = 3.

m2 <- sdmTMB(
  formula = density ~ 0 + as.factor(year) + s(depth),
  data = dat2,
  mesh = mesh2,
  time = "year",
  family = Gamma(link = "log"),
  spatiotemporal = "iid",
  spatial = "on"
)
m2
#> Spatiotemporal model fit by ML ['sdmTMB']
#> Formula: density ~ 0 + as.factor(year) + s(depth)
#> Mesh: mesh2 (isotropic covariance)
#> Time column: year
#> Data: dat2
#> Family: Gamma(link = 'log')
#>  
#>                     coef.est coef.se
#> as.factor(year)2003     4.06    0.20
#> as.factor(year)2004     4.22    0.20
#> as.factor(year)2005     4.19    0.20
#> as.factor(year)2007     3.38    0.20
#> as.factor(year)2009     3.71    0.21
#> as.factor(year)2011     4.51    0.21
#> as.factor(year)2013     4.02    0.19
#> as.factor(year)2015     4.13    0.20
#> as.factor(year)2017     3.84    0.22
#> sdepth                 -0.28    0.36
#> 
#> Smooth terms:
#>            Std. Dev.
#> sds(depth)      1.89
#> 
#> Dispersion parameter: 0.94
#> Matérn range: 0.01
#> Spatial SD: 727.46
#> Spatiotemporal IID SD: 2065.41
#> ML criterion at convergence: 5102.136
#> 
#> See ?tidy.sdmTMB to extract these values as a data frame.
#> 
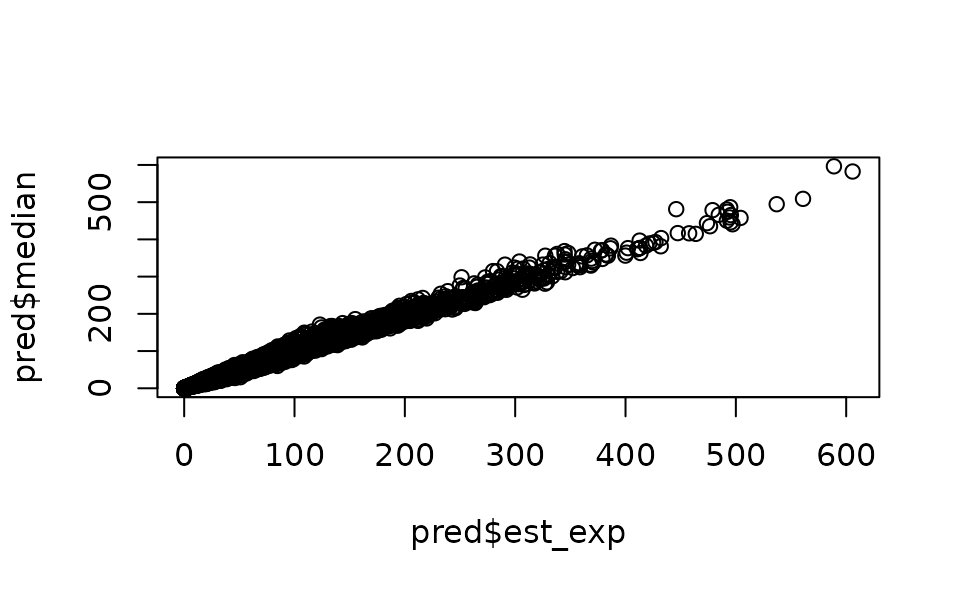
#> **Possible issues detected! Check output of sanity().**

Next, we need some way of combining the predictions across the two models. If all we need are point predictions, we can just multiply the predictions from the two models after applying the inverse link:

pred <- grid_yrs # use the grid as template for saving our predictions
p_bin <- predict(m1, newdata = grid_yrs)
p_pos <- predict(m2, newdata = grid_yrs)
p_bin_prob <- m1$family$linkinv(p_bin$est)
p_pos_exp <- m2$family$linkinv(p_pos$est)
pred$est_exp <- p_bin_prob * p_pos_exp

But if a measure of uncertainty is required, we can simulate from the joint parameter precision matrix using the predict() function with any number of simulations selected (e.g., sims = 500). Because the predictions come from simulated draws from the parameter covariance matrix, the predictions will become more consistent with a larger number of draws. However, a greater number of draws takes longer to calculate and will use more memory (larger matrix), so fewer draws (~100) may be fine for experimentation. A larger number (say ~1000) may be appropriate for final model runs.

set.seed(28239)
p_bin_sim <- predict(m1, newdata = grid_yrs, nsim = 100)
p_pos_sim <- predict(m2, newdata = grid_yrs, nsim = 100)
p_bin_prob_sim <- m1$family$linkinv(p_bin_sim)
p_pos_exp_sim <- m2$family$linkinv(p_pos_sim)
p_combined_sim <- p_bin_prob_sim * p_pos_exp_sim

p_combined_sim is a matrix with a row for each row of data that was predicted on and width nsim. You can process this matrix however you would like. We can save median predictions and upper and lower 95% confidence intervals:

pred$median <- apply(p_combined_sim, 1, median)
plot(pred$est_exp, pred$median)

ggplot(subset(pred, year == 2017), aes(X, Y, fill = median)) +
  geom_raster() +
  coord_fixed() +
  scale_fill_viridis_c(trans = "sqrt")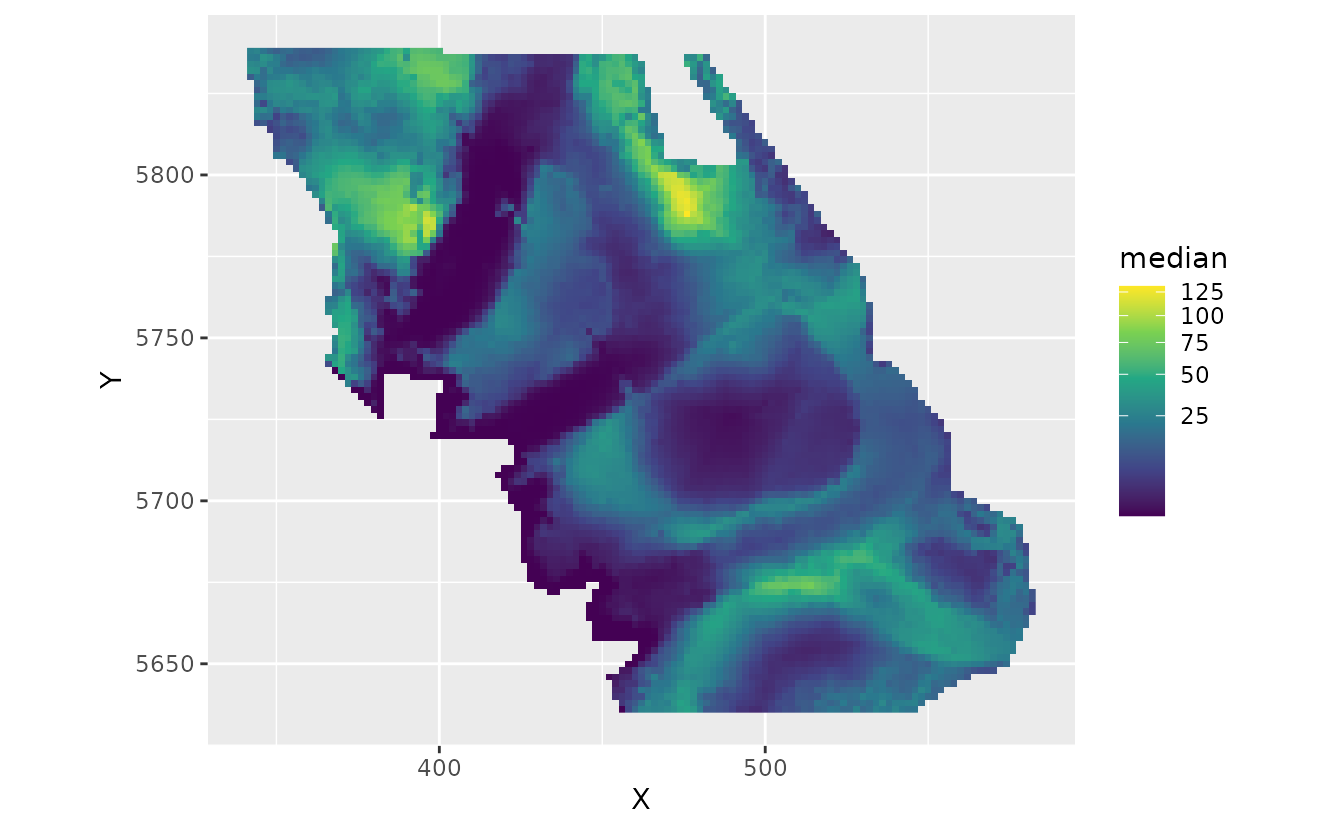

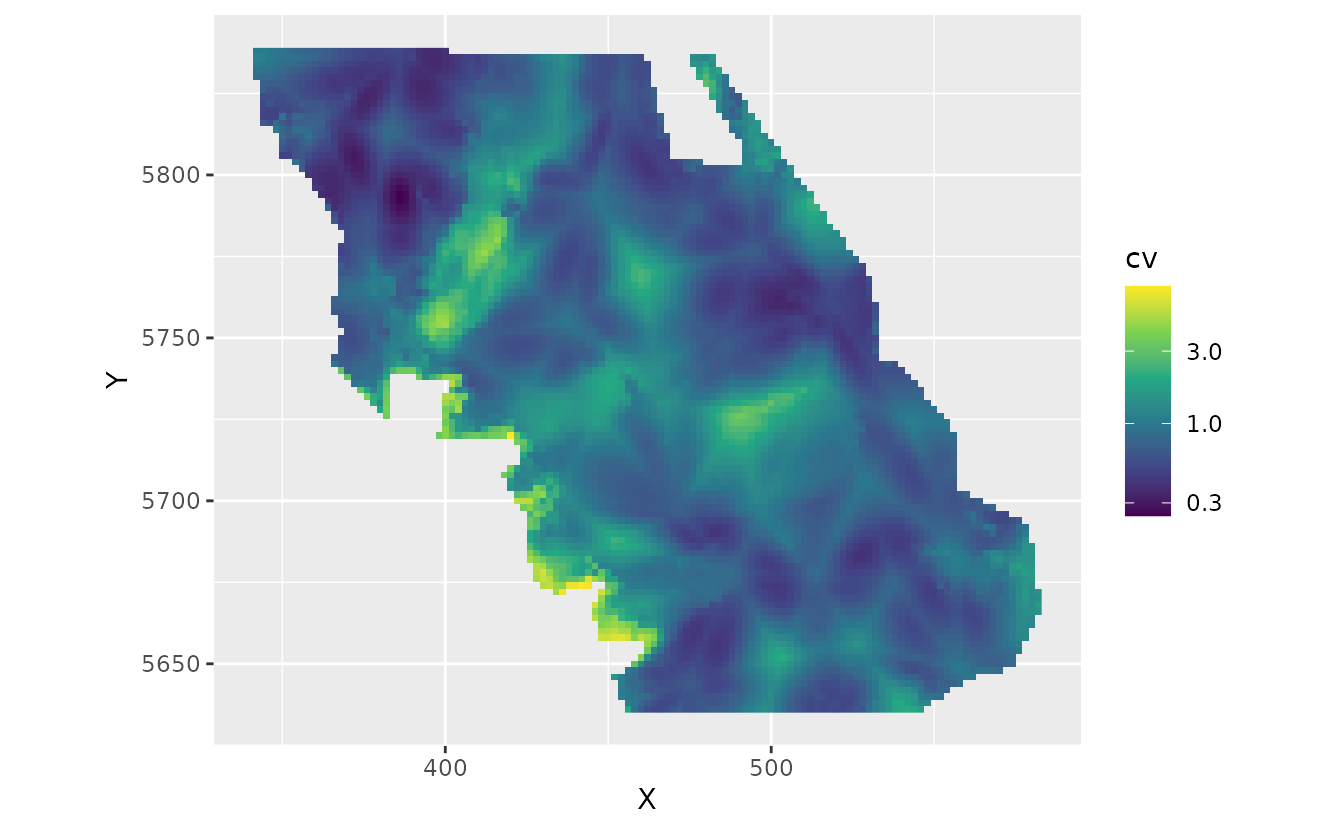
And we can calculate spatial uncertainty:

pred$cv <- apply(p_combined_sim, 1, function(x) sd(x) / mean(x))
ggplot(subset(pred, year == 2017), aes(X, Y, fill = cv)) + # 2017 as an example
  geom_raster() +
  coord_fixed() +
  scale_fill_viridis_c(trans = "log10")

Julia Indivero, Philina English, Sean Anderson, Eric Ward, Lewis Barnett

2024-11-29

Example with built-in delta model

Delta models by fitting two components separately and combining predictions